Characteristics of Estimators

Prerequisites
Measures of Central Tendency, Variability, Introduction to Sampling Distributions, Introduction to Estimation, Degrees of Freedom

Learning Objectives

1. Define bias
2. Define sampling variability
3. Define expected value
4. Define relative efficiency

This section discusses two important characteristics of statistics used as point estimates of parameters: bias and sampling variability. Bias refers to whether an estimator tends to either over or underestimate the parameter. Sampling variability refers to how much the estimate varies from sample to sample.

Have you ever noticed that some bathroom scales give you very different weights each time you weigh yourself? With this in mind, lets compare two scales. Scale 1 is a very high-tech digital scale and gives essentially the same weight each time you weigh yourself; it varies by at most 0.02 pounds from weighing to weighing. Although this scale has the potential to be very accurate, it is calibrated incorrectly and, on average, overstates your weight by one pound. Scale 2 is a cheap scale and gives very different results from weighing to weighing. However, it is just as likely to underestimate as overestimate your weight. Sometimes it vastly overestimates it and sometimes it vastly underestimates it. However, the average of a large number of measurements would be your actual weight. Scale 1 is biased since, on average, its measurements are one pound higher than your actual weight. Scale 2, by contrast, gives unbiased estimates of your weight. However, Scale 2 is highly variable and its measurements are often very far from your true weight. Scale 1, in spite of being biased, is fairly accurate. Its measurements are never more than 1.02 pounds from your actual weight.

We now turn to more formal definitions of variability and precision. However, the basic ideas are the same as in the bathroom scale example.

Bias

A statistic is biased if the long-term average value of the statistic is not the parameter it is estimating. More formally, a statistic is biased if the mean of the sampling distribution of the statistic is not equal to the parameter. The mean of the sampling distribution of a statistic is sometimes referred to as the expected value of the statistic.

As we saw in the section on the sampling distribution of the mean, the mean of the sampling distribution of the (sample) mean is the population mean (μ). Therefore the sample mean is an unbiased estimate of μ. Any given sample mean may underestimate or overestimate μ, but, there is no systematic tendency for sample means to either under or overestimate μ.

In the section on variability, we saw that the formula for the variance in a population is

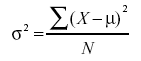
whereas the formula to estimate the variance from a sample is

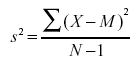
Notice that the denominators of the formulas are different: N for the population and N-1 for the sample. We saw in the "Estimating Variance Simulation" that if N is used in the formula for s2, then the estimates tend to be too low and therefore biased. The formula with N-1 in the denominator gives an unbiased estimate of the population variance. Note that N-1 is the degrees of freedom.

Sampling Variability

The sampling variability of a statistic refers to how much the statistic varies from sample to sample and is usually measured by its standard error ; the smaller the standard error, the less the sampling variability. For example, the standard error of the mean is a measure of the sampling variability of the mean. Recall that the formula for the standard error of the mean is

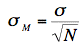
The larger the sample size (N), the smaller the standard error of the mean and therefore the lower the sampling variability.

Statistics differ in their sampling variability even with the same sample size. For example, for normal distributions, the standard error of the median is larger than the standard error of the mean. The smaller the standard error of a statistic, the more efficient the statistic. The relative efficiency of two statistics is typically defined as the ratio of their standard errors. However, it is sometimes defined as the ratio of their squared standard errors.